3.応力テンソルの性質|材料力学
応力テンソルを扱う意義
6つの独立した応力テンソル成分が1セット解っていれば、いろいろな座標系での応力テンソルを求めることができます。しかし、このような任意の応力テンソルを求められることに関して、技術者の立場からすればあまり意義がないかもしれません。技術者にとっては、応力テンソルから任意の方向の応力を抽出することができると言った方が意義があるかもしれません。特にひずみゲージで測定した実験値とFEMで計算した値を比較する場合などは、この考え方についての理解は欠かせません。
本項では応力テンソルとその取り扱い方について考えてみます。
そもそもテンソルとは
テンソルについての数学的定義を調べてみると解りますが、その定義は技術者にとって非常に解りづらいです。ここでは数学的な定義は置いておき、その概念について私の理解を簡単に書いてみたいと思います。(これは技術者としての私の理解であり、正しくない可能性があります)
テンソルには階数0のテンソル、階数1のテンソル、階数2のテンソル・・と数学的にたくさんの種類があります。物理や工学でよく使うのは0〜2までで、それぞれスカラー(階数0のテンソル)、ベクトル(階数1のテンソル)、テンソル(階数2のテンソル)に対応します。スカラーもベクトルもテンソルの仲間なのです。
まずはスカラーについて。スカラーとは値だけを持つ量であり、質量や温度などが挙げられます。当然のことながら、それらは座標系がどうであろうと関係なく定義できます。
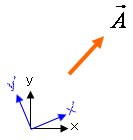
次にベクトルですが、ベクトルは力や速度などのように方向と大きさを持つ量です。まずは図3-1を見てください。Aというベクトルがあるとします。このAベクトルはx-y座標系から見たものと、少し傾いたx'-y'座標系から見たものではベクトル成分の値は異なります。しかし、それを眺めている私たちにとっては、座標系を変えても、依然としてそこに同じ向きと大きさで存在しており、なんら変化はありません。
 |
最後にいわゆるテンソル(階数2のテンソル)です。テンソルは応力やひずみの他にも工学でよく使う慣性モーメントも同様にテンソルとして定義されます。例えば慣性モーメントに関して、座標系を変化させてみると、テンソル成分の中身は変わりますが、物体そのものの慣性という性質が変化することはありません。物体にとって座標系をどう取ろうとまったく関係ありません。
当たり前のことしか言っていませんが、テンソルとはそういうものを定義する量なのです。テンソルとは、座標系にはまったく依存せず、ある物理量を表現する量といえます。しかしそれは見かけ上、座標系を変化させると値が変化して見えることがありますが(スカラーは変わりません)、表現しているものの状態や性質が変化しているわけではないということです。したがってテンソルは、単なる値を3×3の行列表記したものとは本質的に異なる性質を持っています。
なんだか漠然とした説明になってしまいましたが、私たちは数学者ではありませんので、この程度の概念的な理解があれば十分と考えます。興味のある方は数学的な定義を調べてみてください。
座標変換
応力テンソルは、いろいろな座標系で定義したものに簡単に変換することができるという性質があります。これは以下の式(3-1)を用いて計算します。
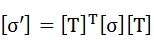 ・・・(3-1)
・・・(3-1)
[σ]:もとの座標系における応力テンソル、[σ']:変換後の座標系で定義される応力テンソル、
[T]:座標変換マトリクス、上付きT:転置
FEMでよく用いられる座標変換マトリクス[T]は、各軸まわりの回転がよく使われ、次式のように定義されます。
x軸まわりの回転 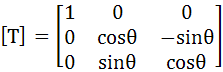 ・・・(3-2)
・・・(3-2)
y軸まわりの回転  ・・・(3-3)
・・・(3-3)
z軸まわりの回転 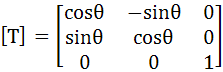 ・・・(3-4)
・・・(3-4)
これにより任意に軸まわりに回転した座標系における応力テンソルを求めることができます。しかし、これ自体は私たちが直接計算したりすることは少ないです。ほとんどがプリポストプロセッサー内部で処理する内容です。
特定の方向の応力を抽出
応力テンソルはすべての応力を計算する元になっています。応力テンソルから主応力やミーゼス応力、あるいは特定の方向の応力を抽出したりすることができます。
まずはコーシーの公式と呼ばれる式(3-5)を紹介します。これはベクトル{n}で定義された面に加わる応力ベクトルを求める式です。
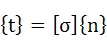 ・・・(3-5)
・・・(3-5)
{t}:ベクトル{n}で定義された面に加わる応力ベクトル、
{n}:参照したい面の法線ベクトル、[σ]:応力テンソル
通常応力というと、面に垂直あるいは平行な方向で定義されますが、応力ベクトルはそれらの方向に分解せず、ベクトルとして表記したものです。この段階で応力ベクトル{t}が参照している座標系は、応力テンソル[σ]と同じです。
ここでさらに応力ベクトル{t}とベクトル{n}の内積をとると、ベクトル{n}の方向成分のみを抽出することができます。これらの処理を一つの式で表したのが式(3-6)です。
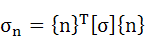 ・・・(3-6)
・・・(3-6)
σn:ベクトル{n}で表される方向の応力値
結局のところ、参照したい方向のベクトルを応力テンソルの両脇から乗じれば、その方向の応力値が抽出されるということです。以下に計算例を示します。
{n}={1,0,0}の場合、つまりx軸方向の応力を計算してみます。これは計算するまでもなく、σxxが答えなのですが、計算の流れを理解するために、はじめは簡単なものでやってみます。
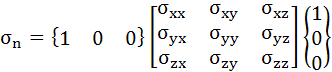 ・・・(3-7)
・・・(3-7)
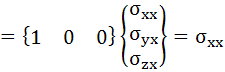 ・・・(3-8)
・・・(3-8)
当然の結果になりましたが、処理内容が理解できたでしょうか。次にちょっとだけ難しくなりますが、{n}={1/√2, 1/√2, 0}の場合です。これはx軸とy軸との成す角が45°の方向を向く大きさ1のベクトルを意味しています。ここで使うベクトル{n}は大きさを1に正規化する必要がありますので、1/√2という中途半端な成分になっていることに注意してください。
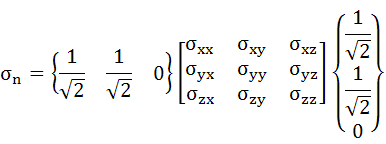 ・・・(3-9)
・・・(3-9)
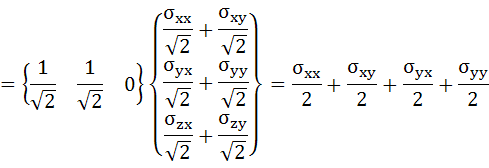 ・・・(3-10)
・・・(3-10)
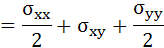 ・・・(3-11)
・・・(3-11)
ちなみに式(3-12)が成り立つことを考慮しています。これについては前項で説明しました。
![]() ・・・(3-12)
・・・(3-12)
このように式(3-6)を用いれば自由にいろいろな方向の応力を簡単に計算することができます。非常に重要な式ですので、これを機会に理解しておくと便利です。この計算方法を知っていると、FEM構造解析における解析結果参照処理を効率的の行うことができます。この辺の話は次項で説明します。
